https://news.mynavi.jp/techplus/article/20240413-2926161/
掲載日
東北大学は4月10日、核子(陽子や中性子)などの複合クォーク粒子である「ハドロン物質」から、ハドロン物質が相互に重なり合うような超高密度物質において開放されるクォークが作るとされる「クォーク物質」へのクロスオーバー領域の物理を記述するべく、「クォーク・ハドロン双対模型」を構築したと発表した。
同成果は、東北大大学院 理学研究科 物理学専攻の古城徹准教授、米・ワシントン大学の藤本悠輝研究員らの国際共同研究チームによるもの。詳細は、米国物理学会が刊行する機関学術誌「Physical Review Letters」に掲載された。
クォークは通常は単体では存在できず、3個セットの「バリオン」か、2個セットの「中間子(メソン)」となり、これらのクォーク複合粒子は「ハドロン」と呼ばれる。ただし、桁外れの圧力が物質に加わると、バリオン内のクォークの自由度が顕在化し、クォークを基本的自由度とする「クォーク物質」になることが予想されている。
そのクォーク物質が存在するかも知れない領域が、半径10kmほどの天体に太陽の1~2倍の質量が詰まった中性子星の中心付近。原子核物理の典型的な密度の単位として、標準核物質密度n0=0.16fm-3が用いられるが、中性子星の中心領域の密度は5n0程度にも達しており、これは核子同士が互いに重なり合うほどに高密度で、クォーク自由度が顕在化している可能性があるという。
中性子星には質量の上限があり(それを超えるとブラックホールになる)、それを決めるのが、物質が持つエネルギー密度(ε)と圧力(P)を関係づける「状態方程式」(EOS)。EOSが「硬い」という場合、考えているエネルギーにおける圧力が大きいことを意味する。
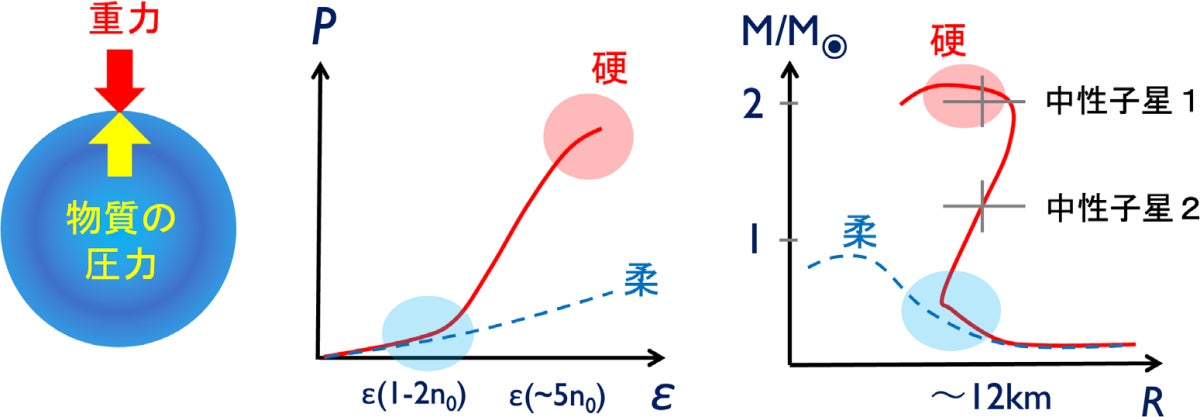
中性子星のEOSと、それに対応して中性子星が取り得る質量と半径の関係。質量-半径曲線は、これまで観測された中性子星が持つ質量と半径を再現する必要がある。中性子星の構造は、その内部のエネルギーが生み出す重力と、物質の圧力との釣り合いによって決定される。エネルギーに比べ圧力が大きい場合、物質は硬い(圧縮しづらい)ので、中性子星のサイズは大きく、取り得る最大質量も大きくなる。ある質量以上では重力崩壊のため、ブラックホールとなってしまう(出所:東北大プレスリリースPDF)
近年、中性子星の質量上限が更新され続けており、現在は太陽質量の約2.1倍に達している。つまり、中性子星内部は従来考えられていたよりもずっと硬い可能性がある。低密度領域においては比較的柔らかいEOSが示唆されているため、なぜEOSが高密度で急激に硬くなるかわかっていなかったとのこと。
そうした中で「ハドロン物質とクォーク物質は滑らかなクロスオーバー転移でつながっている」という考え方が徐々に浸透してきているという。クォークは、低密度ではハドロン同士の相互作用の担い手として現れ、高密度へと向かうにつれ熱力学的における基本的自由度へと進化するのである。しかしクロスオーバー領域を具体的に記述しようとすると、基本的な自由度がハドロンかクォークなのか明確でないことによる困難に直面する。そこで研究チームは今回、同領域の物理を記述すべく、「クォーク・ハドロン双対模型」を構築することにしたという。
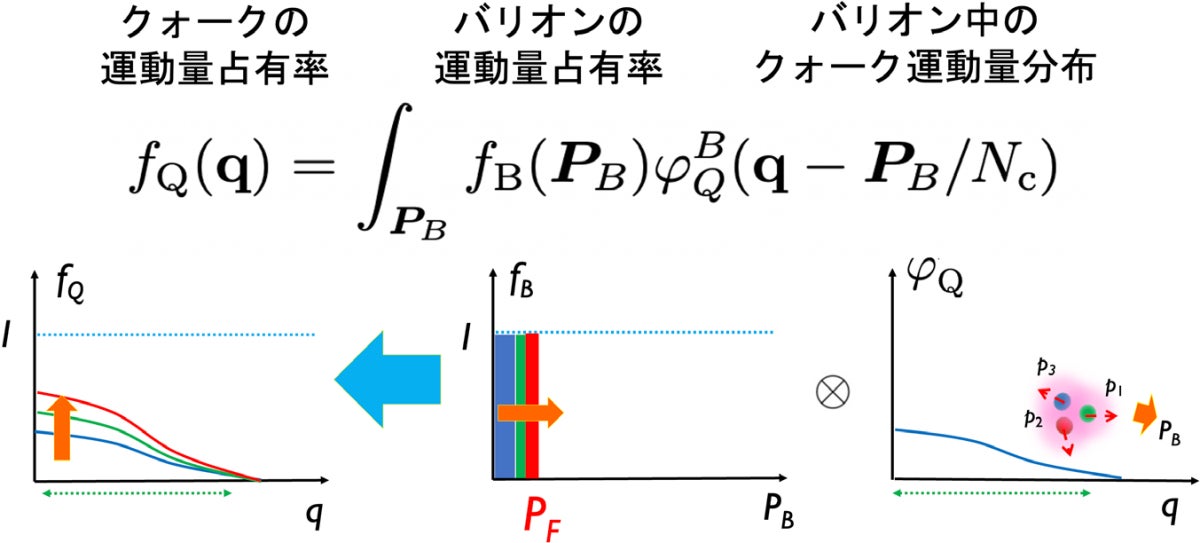
多体系における、クォークの運動量占有率、バリオンの運動量占有率、そしてバリオン単体中のクォーク運動量分布。各バリオンからの寄与を足し上げることでクォークの状態占有率が評価される(出所:東北大プレスリリースPDF)
今回の模型は、クォークとハドロンそれぞれに基づく記述同士が対応付けられ、1つの物理を2つの言語で記述できる点が特徴。クロスオーバー領域のような自由度がはっきりしない領域でも2通りの記述ができるため、ハドロン的効果とクォーク的効果の関係を同時かつ多角的に追っていける。
また、「主要な自由度がどの状態を占有しているか」を示す「状態占有率」により、他粒子系の状態が特徴付けられている(粒子の運動量で状態が特徴付けられた)。状態占有率による記述は、特にバリオンやクォークを多く含む系で有用だという。量子論の基本的性質である「パウリの排他律」により、1つの状態を複数のバリオンやクォークは占有できないが、これは「状態占有率は1を超えられない」という形で取り入れることができるとした。
バリオンはクォーク3つからなる複合系であり、バリオン内部にいるクォークが取る状態を指定すれば、バリオン状態占有率とクォーク状態占有率の間には関係が付く。「ハイゼンベルグの不確定性原理」により、バリオン中で狭い領域に閉じ込められたクォークは、低運動量から高運動量状態まで低い確率で占有している。これら3つの占有率間の関係式が双対模型において最も重要な要素になるという。関係式そのものは単純だが、これをクロスオーバー領域に適用すると、大変非自明な結論が導かれるとする。
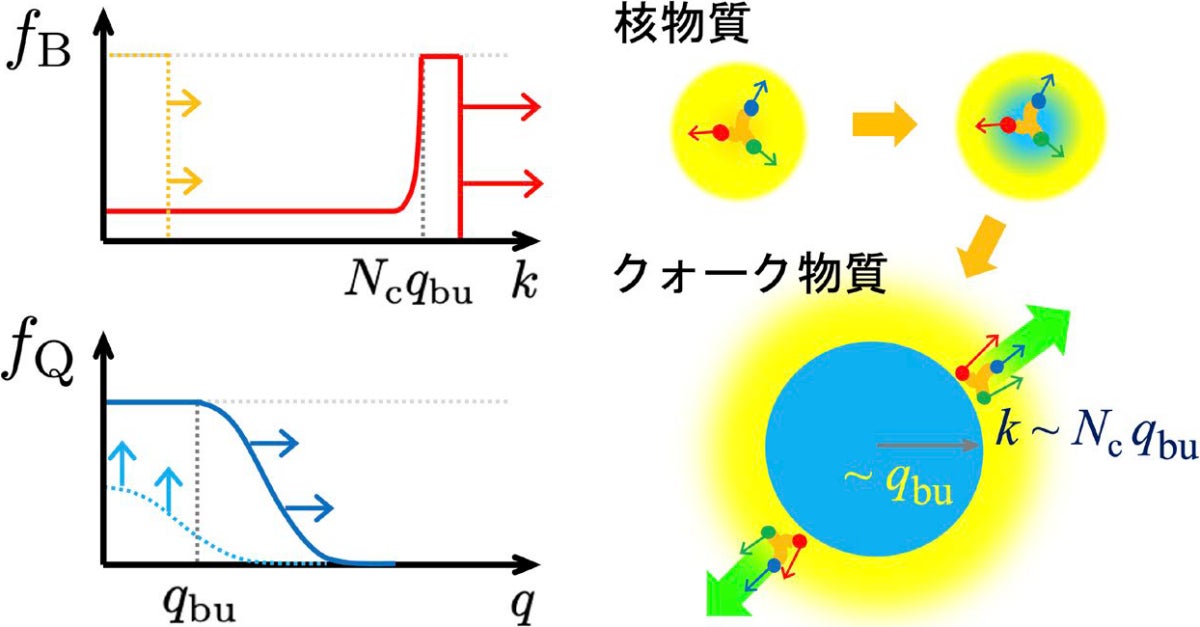
密度が上がった時のバリオンの状態占有率(fB)とクォークの状態占有率(fQ)の変化の様子。状態は粒子の持つ運動量(バリオンはk、クォークはqと記述)で特徴付けられている。点線は低密度の場合の運動量分布、実線は高密度の場合に対応。バリオンの言葉では、低密度ではバリオンは低運動量状態を占有率1で占めているが、高密度になると内部に含むクォークに対するパウリの排他律が効いて、バリオンは高運動量状態へと押し出される(右)。クォークの言葉では、低密度ではクォークの運動量は高運動量まで拡がりを持ち、低運動量状態の占有率は小さいが、高密度になると低運動量状態が飽和し、クォークのフェルミ海ができ、クォーク物質となる(出所:東北大プレスリリースPDF)
低密度領域ではバリオンの方が自然な自由度なので、バリオン占有率をインプットとして与えて、クォーク占有率をアウトプットとする。一方、密度上昇に伴ってクォークの方が自然な自由度となることから、クォーク占有率をインプット、バリオン占有率をアウトプットにすることが望まれるが、これを解くのは一般的に難しいとする。
ただし、バリオン中のクォーク分布の型として、その逆問題を簡単に解けるタイプである「可解模型」が存在する。これは必ずしも現実を定量的なレベルで説明しないが、模型の解析的計算や物理的概念のチェックを可能にするという意味で、その重要性に疑いの余地はないという。今回の研究では、このような可解模型が構築され、バリオン物質からクォーク物質までのEOSの変化を、バリオンとクォークの両方の言葉で記述したとする。そして、バリオン・クォークの状態占有率の発展の仕方は以下の通りとした。
低密度では、バリオン中のクォークは各状態を低い確率でしか占有しないため、バリオンの内部構造の詳細は問題とならず、バリオン状態はほぼ占有率1で低運動量から詰まっていく。しかし密度を上げると、クォークの低運動量状態の占有率は急速に上昇。この領域ではまだバリオンは重くて非相対論的なので、バリオンの数を増やすとエネルギー密度ばかり上昇し、一方で圧力はなかなか増えず、結果としてEOSは柔らかいものとなる。
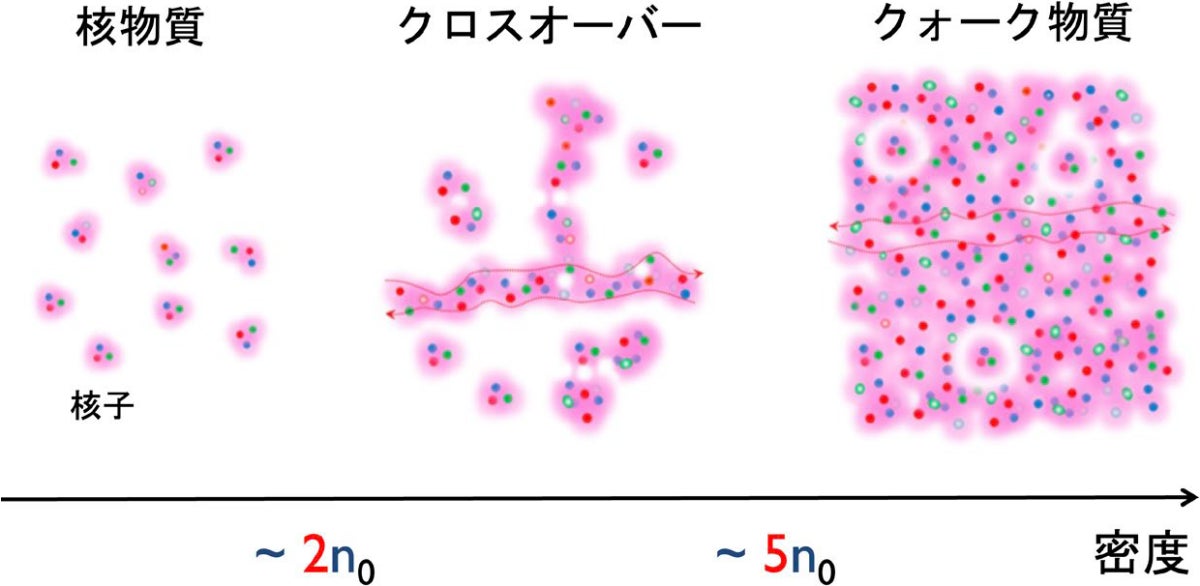
ある密度に到達すると、クォークの低運動量状態が完全に占有され、これ以上の密度ではバリオンのクォーク内部構造を無視できなくなる(これは「クォーク飽和」と命名された)。クォークの内部構造は通常、バリオンが重なると考えられている密度の半分程度(2~3n0)で重要になる。これはバリオンが明確な表面を持った粒子ではなく、「クォークの染み出し」という量子的構造を持っていることによるという。この飽和が起こる領域は、中性子星のEOSが急激に硬くなる領域とほぼ一致する。飽和後は、バリオン内部に閉じていたクォークの相対論的運動に伴う圧力が、系のEOSレベルで見え始める。
さらに密度を上げると、クォークの低運動量状態のかなりの部分が飽和する形でクォークの「フェルミ海」ができる。これは通常のクォーク物質の特徴づけに使われる概念だ。一方、バリオン状態占有率に目を向けると、クォークのパウリ排他律を破らないようにするため、低運動量状態の占有率は低くならざるを得ず、高運動量状態でのみ通常の占有率を取ることが今回の研究の解析計算により示されたという。これは、結局のところパウリ排他律を避ける形でバリオンが相対論的になることが示されており、バリオンの言葉でもクォークの言葉でも相対論的圧力を記述できることが保証されているとした。
研究チームは今後、バリオン間相互作用をクォークレベルで記述する研究やクォーク物質中でのハドロン相関を議論する研究が重要になっていくことが考えられるとしている。








0 コメント:
コメントを投稿